Skip List是一个基于链表的概率数据结构,是平衡树的简单且有效的替代品。为什么说是概率数据结构,这体现在skip list的创建和search上。
传统的链表很难快速跳转至某一个节点,所以查找也是很耗时的(即使这是一个有序的链表),skip list则解决这些问题,并且查找的时间复杂度是O(log n),所以skip list在lucene中也是一大利器。
下图就是一个skip list示例:
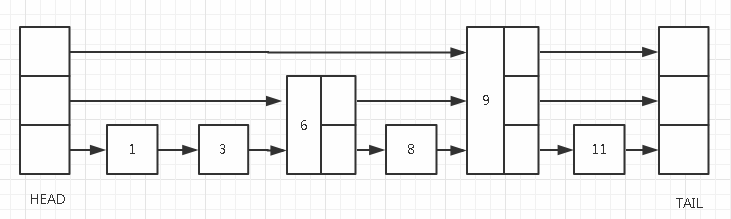
一个标准的跳跃表,至少要有HEAD、TAIL节点,即头节点和尾节点。如果这是一个节点递增的链表,那么HEAD节点元素小于skip list中任何一个节点元素、TAIL节点元素大于任何一个其它节点元素。
每一个节点至少含有一个指向下一个节点的指针,节点的level大小决定了指针个数,也就决定了该节点的跳跃性,如果level=1,那么该节点只能直接访问下一个节点,如果level>1,那么该节点可能快速的跳跃至其之后的某个节点。
HEAD、TAIL的level=MaxLevel,即头节点和尾节点的level大小为skip list设置的最大level,这个性质实际上很有用,后面我们具体说。
创建
我们先来看一下skip list节点的定义:
public class ListNode {
ListNode[] forwords;
int value;
public ListNode(int level, int value) {
this.forwords = new ListNode[level];
this.value = value;
}
}
是不是贼简单,节点值、以及指向后续节点的多级指针。
知道节点的数据结构,下面我们继续看怎么构建一个skip list,首先我们构建一个空的skip list,只含有HEAD、和TAIL节点。
public class SkipList {
private ListNode HEAD;
private ListNode TAIL;
private int maxLevel;
private int currentLevel = 1;
public SkipList(int maxLevel) {
this.maxLevel = maxLevel;
this.HEAD = new ListNode(maxLevel, Integer.MIN_VALUE);
this.TAIL = new ListNode(maxLevel, Integer.MAX_VALUE);
for (int i = 0; i < maxLevel; i++) {
this.HEAD.forwords[i] = TAIL;
}
}
}
大致逻辑就是分别创建HEAD、TAIL节点,这两个节点的level设置为maxLevel,即有maxLevel个指针,HEAD节点多级指针都是指向TAIL节点。
这里涉及到一个问题,我们如何设置maxLevel,因为level决定了skip list的查找性能, 可能我们直观上会认为level越大,跳跃约灵活,但是这是相对的,如果skip list中只有8个元素,而level却设置成8,那反而是一种浪费,而如果level设置为1,那和普通的链表也没啥区别,那到底怎么设置maxLevel呢,等我们看完insert节点活说到。
但是说insert之前,我们先说skip list如何查找元素,因为不管是插入和删除,都逃不了对skip list的查找。以上图的skip list为例,我们查找元素8。
查找
首先我们找到了HEAD节点,发现HEAD节点的level3指针指向节点9,而9大于我们想找的8,也就是8在9这个节点之前。
我们将level降一级,找HEAD的level 2指针,该指针指向节点6,6是小于8的,继续看节点6的level 2指针,也是指向9,所以还得降level,继续看节点6的level 1指针。
节点6的level 1指针的下一个节点是8,也就是我们要找的元素。
如果我们要找的是7,在找到节点6的level 1指针后,发现下一个节点8大于7,level已经没法在降了,所以直接返回空节点。
search节点的代码如下:
public ListNode search(int key) {
ListNode x = HEAD;
for (int level = currentLevel - 1; level >= 0; level--) {
while (x.forwords[level].value < key) {
x = x.forwords[level];
}
}
return key == x.forwords[0].value ? x.forwords[0] : null;
}
插入
如果在skip list中插入一个节点,假如我们要在skip list插入7,我们首先找到了6这个节点,因为7即将插在6和8之间,我们需要注意一个事情,如果是一个普通链表,插入一个新节点我们需要将6和8之间的执指针断开,但是对于skip list而言,如果插入的节点level>1的话,可能需要调整level2、level3上的指针。
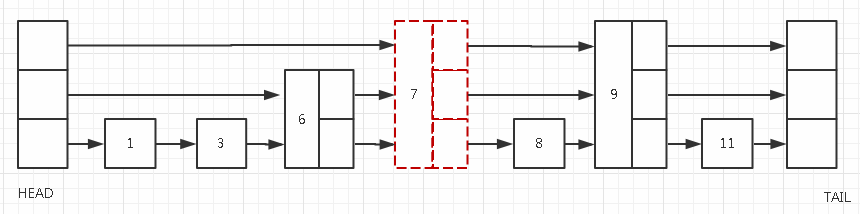
假如新插入的节点7的level=3(如上图),那么我们需要在search的时候,就将它的前继节点,也就遍历到7之前,需要在level 3上遍历的最后一个节点(HEAD节点)、level 2上最后一个节点(节点6)、level 1上最后一个节点(节点6)。分别断开HEAD节点到节点9的指针、节点6到节点9指针、节点6到节点8的指针,在之间插入节点7。
插入节点的代码如下:
public ListNode insert(int key) {
ListNode[] preNodes = new ListNode[maxLevel];
ListNode x = HEAD;
for (int level = currentLevel - 1; level >= 0; level--) {
while (x.forwords[level].value < key) {
x = x.forwords[level];
}
preNodes[level] = x;
}
if (x.forwords[0].value == key) {
return x.forwords[0];
}
int nodeLevel = randomLevel();
if (nodeLevel > currentLevel) {
for (int i = currentLevel; i < nodeLevel; i++) {
preNodes[i] = HEAD;
}
currentLevel = nodeLevel;
}
ListNode newNode = new ListNode(nodeLevel, key);
for (int i = 0; i < nodeLevel; i++) {
try {
newNode.forwords[i] = preNodes[i].forwords[i];
preNodes[i].forwords[i] = newNode;
} catch (Exception e) {
System.out.println(e.getMessage());
}
}
return newNode;
}
level大小
那么我们怎么设置一个节点的level呢,因为level决定了跳跃表的跳跃性,显然根据数据分布的设置每个节点的level是最好的,但是这种代价太大了,可行性太低了。
假如level为1,那么和普通的链表并没有什么区别。假如所有节点的level都是相等的,那么和普通链表也没什么区别,反而造成了空间浪费。
既然这样,我们就想能不能一层节点和多层节点各占到一半。skip list是一个概率数据结构,这就体现在level的创建上,我们可以借助概率分布的思想决定每一个新节点的level大小,就像每次在创建一个新的节点时候,我抛一个硬币,正面的level=1,反面level>1,好吧,这只是一个简单的例子,通常的skiplist的level不太可能只是2,我们更加希望看到的是有某个节点level=i,该节点还存在level=i+1的概率是50%,这样才能保证构建的skip list更加平衡高效,至少有一半节点的level>1,但是level>2的节点只是level=1节点的一半,以此类推。
节点level大小代码如下:
private int randomLevel() {
// 概率P,用于控制多层节点的分布概率
float p = 0.5f;
int level = 1;
Random random = new Random();
while (random.nextInt(10) / 10f < p && level < maxLevel) {
level++;
}
return level;
}
既然说到这了,顺便再提一下MaxLevel如何设置,因为level i+1是level i节点数的1/2,所MaxLevel接近log(n),假如n=8,那么MaxLevel=3,第一级4个元素,第二级2个元素,第三级1个元素。
删除
最后我们再说一下节点的删除,与插入一样,我们同样需要先找到要删除的节点,例如删除节点9,我们需要先找到遍历到节点9之前,level 3上的前一个节点(节点HEAD)、level 2上的前一个节点(节点6)、level 1上的前一个节点(节点8),然后断开这几个节点与节点9的指针,与节点9各个level上的后继节点连接。
如图:
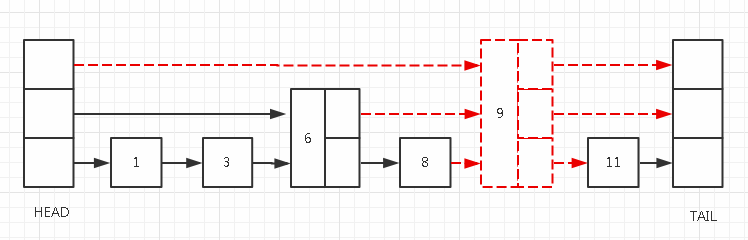
当然有一点我们要注意,在插入节点的时候,新节点的level高于其他节点level(除HEAD、TAIL),我们将当前skip list的level设置为该节点的level。而对于删除而言,我们同样需要更新当前skip list的level,当时这稍微比插入时的level更新要复杂点,但是如果知道了开头我提到的那个特性之后,其实也不难,也就是说HEAD和TAIL的level=MaxLevel,在skip list中不存在level为MaxLevel的节点情况下,HEAD节点再MaxLevel上的指针是直接可以指向TAIL节点的,如果当前skip list中的其它节点(除去HEAD和TAIL)最大的level为1,那HEAD的level 2指针直接就是指向TAIL节点。
具体看一下代码:
public ListNode delete(int key) {
ListNode[] preNodes = new ListNode[maxLevel];
ListNode x = HEAD;
for (int level = currentLevel - 1; level >= 0; level--) {
while (x.forwords[level].value < key) {
x = x.forwords[level];
}
preNodes[level] = x;
}
if (x.forwords[0].value != key) {
return null;
}
x = x.forwords[0];
int delLevel = x.forwords.length;
for (int i = 0; i < delLevel; i++) {
preNodes[i].forwords[i] = x.forwords[i];
}
// 更新level
while (currentLevel > 1 && HEAD.forwords[currentLevel - 1] == TAIL)
currentLevel--;
return x;
}
本文的所有代码可在我的GITHUB找到:SkipList.java