本文用例引用至 product-quantizer-tutorial

目前最近邻搜索主要有如下方法：

  • 线性查找，复杂度：O(Nd)O(Nd) ,其中N为向量集大小，d为向量的维度
  • 空间分割，KD树

而高纬向量的NN Search（Nearest neighbor Search）因为维度爆炸，成本非常高，在KNN算法中，我们常用KD树来加快最近邻节点的查找，KD树主要分为树的构建和查找两部分：

KD树构建：

  • 特征选择与数据划分，因为距离度量一般采用曼哈顿距离，所以通常我们会选择对距离计算影响较大的特征作为划分标准，所以自然而言会采用计算数据集中n个特征的方差，选取方差较大的特征计算均值进行划分
  • 对左集合右集递归划分

KD树搜索最近邻：

  • 搜索到叶子节点
  • 按搜索路径向上回溯
  • 更新最近邻，在回溯的过程中，需要确认另外一个子节点是否需要加入搜索路径中进行回溯，判断的标准就是目标点到父节点为半径的圆能否覆盖父节点的另一个子节点。

虽然使用了KD树进行特征分割，但是如果数据分布不是很好，同样会存在穷举所有向量的可能性，点积量化是向量量化的一种，用于加速最近邻搜索。

量化在信息论中被广泛研究应用，它是对信息破坏的过程，目的是减少表征空间的基数。对于一个D维的向量 x∈RDx\in R^D，将其分区为{V0,V1,..,Vi,..,Vk−1}\{V_0,V_1,..,V_i,..,V_k-1\} K个子集，ViV_i 称为一个单元(cell)，量化器就是用函数qq将向量映射为q(x)∈C={ci;i∈I}q(x)\in C=\{c_i;i \in I\}，I=0...k−1I=0...k-1，cic_i为ViV_i 的质心（centroid）。例如一张图片构建一个颜色的映射函数，将图片中24-bit RGB颜色值转为一个8-bit的整型。

点积量化

假如我们有50000张图片，并且我们已经使用卷积神经网络进行了特征的抽取，然后我们得到了50000个特征向量，每个特征向量维度为1024。
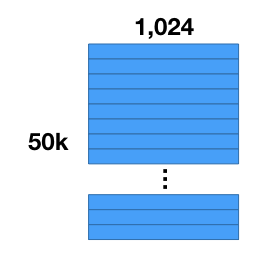
pq-image_vectors

量化

我们要对数据集进行压缩，那么如何进行压缩，将向量集分割成8个子集，每个子集中向量维度变为128，也就是将数据集分割成8个[5000x128][5000x128]的矩阵。

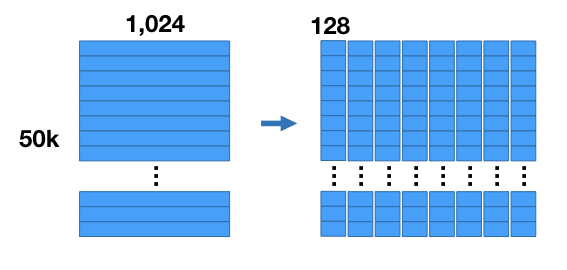
pq-vector_slice

紧接着，对每个矩阵使用k-means进行聚类，k=256，这样这8个子集都会产生256个质心（centroid，这256质心称为codebook，8个子集对应8个codebook,每个质心称为code），也就是数据集会被压缩成8个[256x128][256x128]的矩阵。

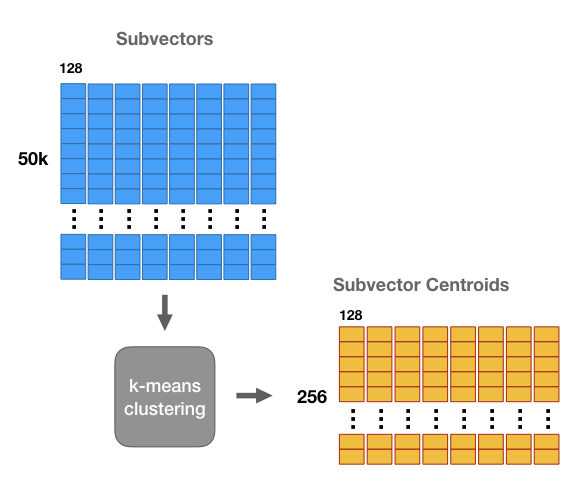
pq-kmeans_clustering

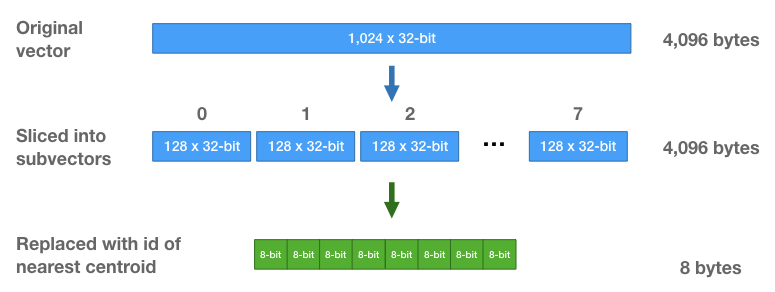
与直接存储原来的浮点值相比，我们只需要存储向量的ID，对于子集中每个向量，我们找到与它最近的质心（centroid），然后存储该质心对应的id。

而对于每个向量而言，将使用8个质心ID所代替。对于8个子集的中每个子集，我们使用256个质心ID去表示，所以对于每个子集只需要8 bits去存储一个质心ID,原先，对于每一个向量，我们需要使用1024∗4bytes=4096bytes1024*4 bytes=4096 bytes进行存储，而现在每个向量我们只需要8个8 bits的整型去存储，即每个向量8 bytes。
pq-compression

在product-quantizer-tutorial中，作者给出了一种NN Search的方案，暂且说一下该方法：

经过量化之后，向量集中每个向量都使用8个质心进行表示，那么给定一个1024维的Query向量qq，首先我们将Query向量分成8个128维的向量:{qi，i∈[0,7]}\{q_i，i \in [0,7]\}，遍历50000个量化后的向量，分别计算qiq_i到每个向量8个质心的距离：∑i=07(qi,ci)2\sqrt{\sum_{i=0}^7(q_i,c_i)^2}，cic_i为数据集中该向量i部分关联的质心。

query向量会计算得到与向量集中每个向量的一个近似距离，最后返回最近邻的k个向量，其实我们不难发现，我们计算的复杂度还是50000x8x128（每个质心实际上还是128维），非常高，但是呢，向量集中的质心（c）只有8x256个，上面工式中的qiq_i也只存在8中情况，那理论上我们的计算复杂度只有8x256x128，其实再仔细分析一下，那是因为存在重复计算，也就是做个cache就好。

但对于一个有搜索背景的同学，我们肯定会想到通过倒排的进行解决，也就是说经过量化，向量集中的每个向量都可以使用8个质心进行表示，我们对向量进行ID编码，建立质心到属于该质心向量ID的倒排链。
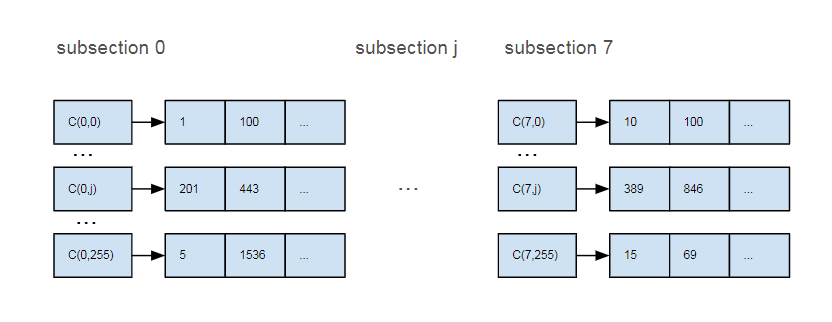
pq-postlist

对于query向量，我们只需要从每个subsection选出距离最近的质心，然后将每个质心对应的倒排链求交，拿出来向量就是最近邻的向量，并且我们还可以对这些向量再做精确的距离运算。

【product-quantizer-tutorial】 (http://mccormickml.com/2017/10/13/product-quantizer-tutorial-part-1)
【jegou_searching_with_quantization】 (https://lear.inrialpes.fr/pubs/2011/JDS11/jegou_searching_with_quantization.pdf)