当我们在电商网站上搜索一个关键词想买一个东西的,例如:“appe”这个词,但是这个词对于电商网站来说,并没有相应的商品,但是如果直接返回空的列表页的话,用户体验还是相当差的,所以通常电商网站上会给出:
- 你是不是想搜索“apple”
- 直接返回apple对应的结果
这其实就是拼写纠错。
那么怎么能从appe关联到apple呢,往简单点说,就是appe和apple两个词的相似度很高,那怎么去衡量两个词的相似度呢,这就是我们今天要讲的编辑距离。
原谅我的孤陋寡闻,只能从脑海出检索出apple和appe相关了
本文只考虑Levenshtein,因为常见的编辑距离还有汉明距离(对于两个相等长度字符串,所需要的替换次数),最长公共子串距离。
定义
给定字符串S1和目标字符串S2,允许插入字符、删除字符、替换字符三种编辑操作,S1最少需要做多少次编辑可以变成S2。那么这最少的编辑次数就是编辑距离。
编辑距离实际上是动态规划的一种,也就是说可以把问题的最优归为子问题的最优,下面我们就说说怎么把一个大问题变成若干个小问题,在这之前我们先给出如下符号定义:S1(i)为字符串S1的第i个字符,D(i,j)表示S1的前i个字符与S2的前j个字符的编辑距离。
我们再分以下情况来讨论:
- 假如字符串S1和S2有一个为空串,那么他们的编辑距离为非空字符串的长度,即D(0,j)=j、D(i,0)=i
- 假如两个字符串都不为空,同样存在两种情况:
2.1 如果S1(i)=S2(j),即存在D(i,j)=D(i-1,j-1),这点应该很好理解。
2.2 如果S1(i)!=S2(j),有一点可以肯定的D(i,j)=min(D(i-1,j-1),D(i-1,j),D(i,j-1))+1,即可能为S1(i)位置进行替换,S(i-1)之后插入,S(i)位置删除。例如:S1=“cat”和S2=“can”:
- D(2,1),即ca变换到c,需要删除S1(2),即为D(1,1)+1
- D(2,3),即ca变换到can,需要在ca后面插入n,即D(i,j-1)+1
- D(3,3),即cat变换到can,需要将t替换为n,即D(i-1,j-1)+1
好,这样我们的问题就变得简单的,求D(i,j)可以变换为求D(i-1,j)、D(i,j-1)、或者D(i-1,j-1),再递推就是d(0,1)、d(1,0)或者d(0,0)
实现
那么我们则可以给出我们的程序:
public int[][] distanceMatrix(String word1, String word2) {
int[][] distance = new int[word1.length() + 1][word2.length() + 1];
for (int i = 0; i < word2.length() + 1; i++)
// word1的0位置变换到word2的前i个字符都要进行i次的插入,所以编辑距离为i
distance[0][i] = i;
for (int i = 1; i < word1.length() + 1; i++) {
distance[i][0] = i;
for (int j = 1; j < word2.length() + 1; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1))
distance[i][j] = distance[i - 1][j - 1];
else
distance[i][j] = min(distance, i, j) + 1;
}
}
return distance;
}
其实上面的程序就是在构建两个字符串的转换矩阵,我们还是以apple和appe为例,函数返回的二维数组应该是这样的:
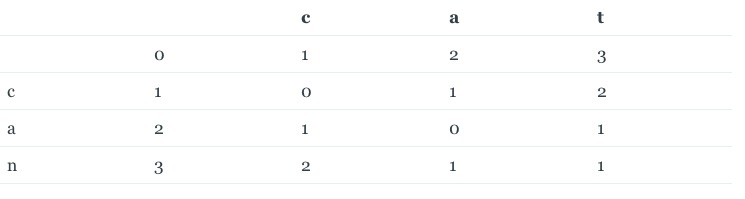
我们不难发现我们每次计算都要构建字符串的转换矩阵,这其实是一种浪费,因为D(i,j)最多只跟D(i-1,j-1)或者D(i-1,j)有关,所以我们没有必要S1的前i-2个串和S2的编辑距离,所以这个算法其实还是可以优化的,具体代码可以参考:EditDistance
这篇文章中我只给出了编辑距离,它离拼写纠错还有一点距离,因为实际场景中我们不可能挨个计算和词典中每个词的编辑距离,从而给出最优的纠错词。在下一篇文章中我将给出拼写纠错的实现。
That's all!
参考《算法笔记-刁瑞/谢妍》